MOS-FET(Pch&Nch)のハーフブリッジ回路の貫通電流対策用にとスイッチング出力の細かなタイミング調整が出来そうなTCDを試してみた。
通常のPWMは同期動作なので制御精度は周辺クロック(最大24MHz)までであるがTCDは出力も含めて非同期動作なのでPLLクロックの精度(最大48MHz)で制御できる。
高速クロックなCPUは色々あれど、非同期で最大48MHzでGPIO駆動できるのはAVR-DA/DB/DDのみかも...ある意味最強か!!
【ハイサイド(黄色)/ローサイド(水色)用の2つの波形生成が可能】
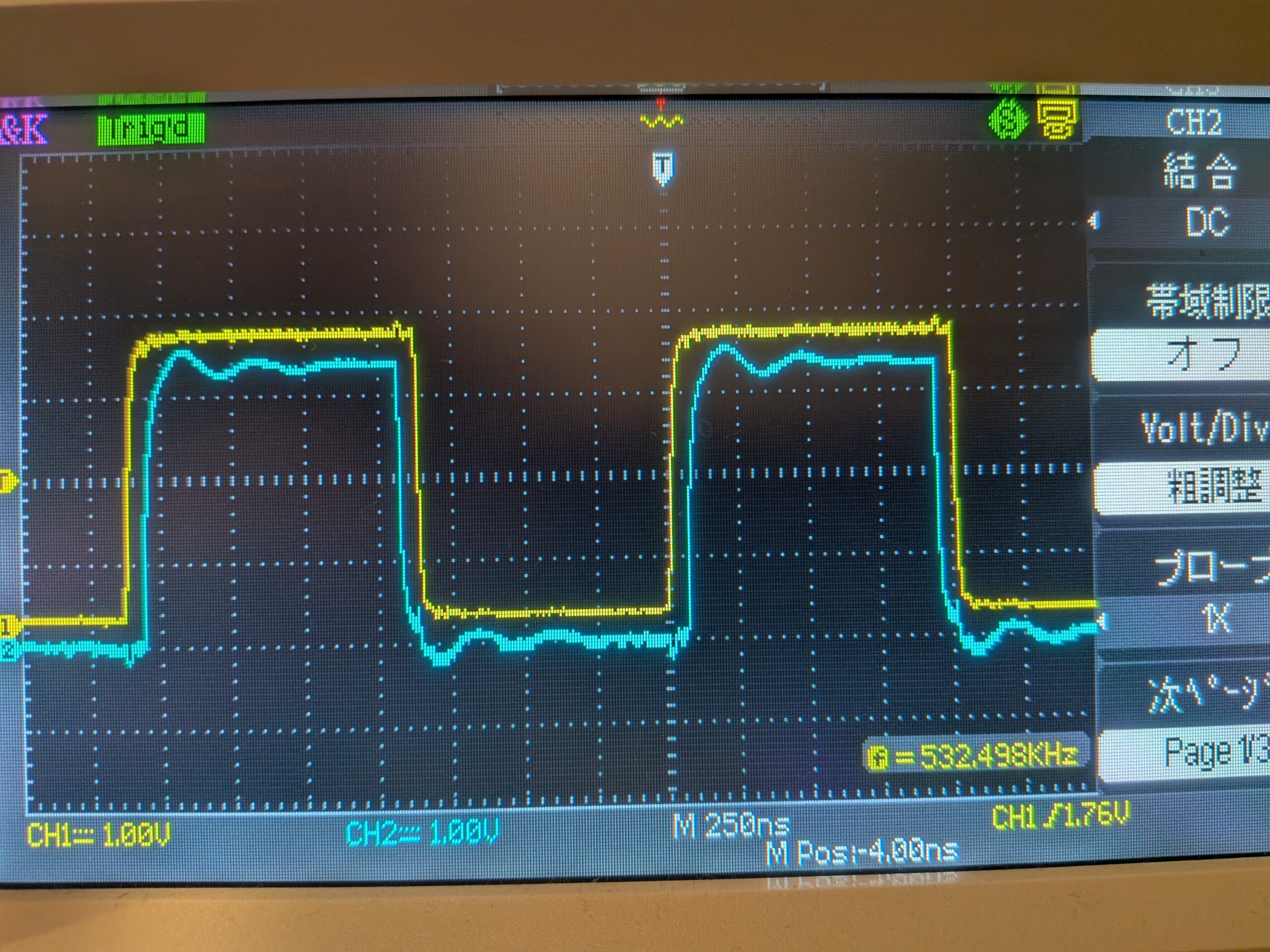
【タイミング調整は最小約20ns(PLL48MHz駆動時)】
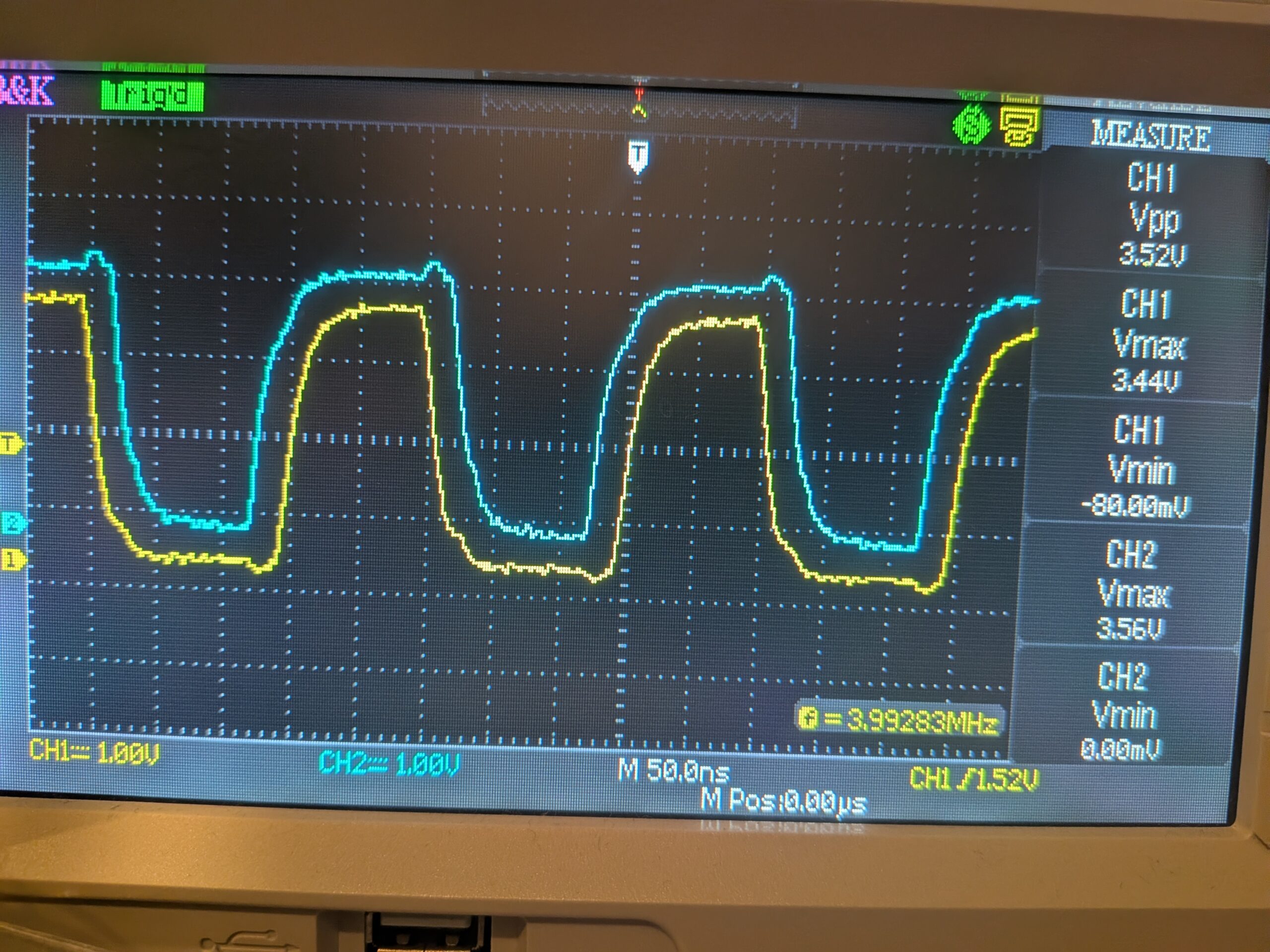
【サンプル】
立上がり/立下りのデッドタイムをTcd:pwm(…)の最後の2つのパラメタ(カウンタークロック数指定)により制御できる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
#include "avr8-tcd.h" #define RISE 2 /* 立ち上がりのデッドタイム */ #define FALL 1 /* 立ち下がりのデッドタイム */ int main(void) { #if 0 /* OSCHFクロック駆動 */ Tcd::begin(Tcd::WGMODE_ONERAMP); #else /* PLLクロック駆動(48MHz) */ Clock::pll(); Tcd::begin(Tcd::WGMODE_ONERAMP, Tcd::CLKSEL_PLL); #endif Tcd::output(Tcd::CMPA, true); /* WOA */ Tcd::output(Tcd::CMPB, true); /* WOB */ Tcd::pwm(Tcd::count(500000), Tcd::MAX_COUNT >> 1, RISE, FALL); Tcd::run(); while (1) yield(); return 0; } |
【修正履歴】
2026-02-22
今日はにゃんにゃんにゃんの日なのでTCDのAUPDATE機能を有効化。って全く関係ありませんけど。(笑)
2026-02-14
CONFIG_TCD_ISRの判定ミスを修正。
2026-02-11
定義名が間違っていたので修正。DLYPRESC_DIV3⇒DLYPRESC_DIV4。
2026-02-10
AVR-1系への対応とメソッド名が間違っていたので修正。capturea()⇒capture()
【ライブラリ】
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 |
/* avr8_tcd.h - TCD Driver for Microchip AVR8 Series Copyright (c) 2026 Sasapea's Lab. All right reserved. This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with this program. If not, see <https://www.gnu.org/licenses/>. */ #pragma once #include "avr8_config.h" #include "avr8_clock.h" #if defined(TCD0) class Tcd { public: static const uint16_t MAX_COUNT; typedef enum { CMPA, CMPB, CMPC, CMPD } CMP; /* Clock select */ typedef enum { #if defined(__AVR_1__) CLKSEL_OSCHF = TCD_CLKSEL_20MHZ_gc, /* 20 MHz oscillator */ CLKSEL_EXTCLK = TCD_CLKSEL_EXTCLK_gc, /* External clock */ CLKSEL_CLKPER = TCD_CLKSEL_SYSCLK_gc /* System clock */ #else CLKSEL_OSCHF = TCD_CLKSEL_OSCHF_gc, /* Internal High-Frequency Oscillator */ CLKSEL_PLL = TCD_CLKSEL_PLL_gc, /* PLL */ CLKSEL_EXTCLK = TCD_CLKSEL_EXTCLK_gc, /* External Clock */ CLKSEL_CLKPER = TCD_CLKSEL_CLKPER_gc /* Peripheral Clock */ #endif } CLKSEL; /* Synchronization prescaler select */ typedef enum { SYNCPRES_DIV1 = TCD_SYNCPRES_DIV1_gc, /* Selected clock source divided by 1 */ SYNCPRES_DIV2 = TCD_SYNCPRES_DIV2_gc, /* Selected clock source divided by 2 */ SYNCPRES_DIV4 = TCD_SYNCPRES_DIV4_gc, /* Selected clock source divided by 4 */ SYNCPRES_DIV8 = TCD_SYNCPRES_DIV8_gc /* Selected clock source divided by 8 */ } SYNCPRES; /* Counter prescaler select */ typedef enum { CNTPRES_DIV1 = TCD_CNTPRES_DIV1_gc, /* Sync clock divided by 1 */ CNTPRES_DIV4 = TCD_CNTPRES_DIV4_gc, /* Sync clock divided by 4 */ CNTPRES_DIV32 = TCD_CNTPRES_DIV32_gc /* Sync clock divided by 32 */ } CNTPRES; /* Delay prescaler select */ typedef enum { DLYPRESC_DIV1 = TCD_DLYPRESC_DIV1_gc, /* No prescaling */ DLYPRESC_DIV2 = TCD_DLYPRESC_DIV2_gc, /* Prescale with 2 */ DLYPRESC_DIV4 = TCD_DLYPRESC_DIV4_gc, /* Prescale with 4 */ DLYPRESC_DIV8 = TCD_DLYPRESC_DIV8_gc /* Prescale with 8 */ } DLYPRESC; /* Waveform generation mode select */ typedef enum { WGMODE_ONERAMP = TCD_WGMODE_ONERAMP_gc, /* One ramp mode */ WGMODE_TWORAMP = TCD_WGMODE_TWORAMP_gc, /* Two ramp mode */ WGMODE_FOURRAMP = TCD_WGMODE_FOURRAMP_gc, /* Four ramp mode */ WGMODE_DS = TCD_WGMODE_DS_gc /* Dual slope mode */ } WGMODE; /* Dither select */ typedef enum { DITHERSEL_ONTIMEB = TCD_DITHERSEL_ONTIMEB_gc, /* On-time ramp B */ DITHERSEL_ONTIMEAB = TCD_DITHERSEL_ONTIMEAB_gc, /* On-time ramp A and B */ DITHERSEL_DEADTIMEB = TCD_DITHERSEL_DEADTIMEB_gc, /* Dead-time rampB */ DITHERSEL_DEADTIMEAB = TCD_DITHERSEL_DEADTIMEAB_gc /* Dead-time ramp A and B */ } DITHERSEL; /* Compare C output select */ typedef enum { CMPCSEL_PWMA = TCD_CMPCSEL_PWMA_gc, /* PWM A output */ CMPCSEL_PWMB = TCD_CMPCSEL_PWMB_gc /* PWM B output */ } CMPCSEL; /* Compare D output select */ typedef enum { CMPDSEL_PWMA = TCD_CMPDSEL_PWMA_gc, /* PWM A output */ CMPDSEL_PWMB = TCD_CMPDSEL_PWMB_gc /* PWM B output */ } CMPDSEL; /* Event config select */ typedef enum { CFG_NEITHER = TCD_CFG_NEITHER_gc, /* Neither Filter nor Asynchronous Event is enabled */ CFG_FILTER = TCD_CFG_FILTER_gc, /* Input Capture Noise Cancellation Filter enabled */ CFG_ASYNC = TCD_CFG_ASYNC_gc /* Asynchronous Event output qualification enabled */ } CFG; /* Event Input Edge select */ typedef enum { EDGE_FALL_LOW = TCD_EDGE_FALL_LOW_gc, /* The falling edge or low level of event generates retrigger or fault action */ EDGE_RISE_HIGH = TCD_EDGE_RISE_HIGH_gc /* The rising edge or high level of event generates retrigger or fault action */ } EDGE; /* Event action select */ typedef enum { ACTION_FAULT = TCD_ACTION_FAULT_gc, /* Event trigger a fault */ ACTION_CAPTURE = TCD_ACTION_CAPTURE_gc /* Event trigger a fault and capture */ } ACTION; /* Input mode select */ typedef enum { INPUTMODE_NONE = TCD_INPUTMODE_NONE_gc, /* Input has no actions */ INPUTMODE_JMPWAIT = TCD_INPUTMODE_JMPWAIT_gc, /* Stop output, jump to opposite compare cycle and wait */ INPUTMODE_EXECWAIT = TCD_INPUTMODE_EXECWAIT_gc, /* Stop output, execute opposite compare cycle and wait */ INPUTMODE_EXECFAULT = TCD_INPUTMODE_EXECFAULT_gc, /* stop output, execute opposite compare cycle while fault active */ INPUTMODE_FREQ = TCD_INPUTMODE_FREQ_gc, /* Stop all outputs, maintain frequency */ INPUTMODE_EXECDT = TCD_INPUTMODE_EXECDT_gc, /* Stop all outputs, execute dead time while fault active */ INPUTMODE_WAIT = TCD_INPUTMODE_WAIT_gc, /* Stop all outputs, jump to next compare cycle and wait */ INPUTMODE_WAITSW = TCD_INPUTMODE_WAITSW_gc, /* Stop all outputs, wait for software action */ INPUTMODE_EDGETRIG = TCD_INPUTMODE_EDGETRIG_gc, /* Stop output on edge, jump to next compare cycle */ INPUTMODE_EDGETRIGFREQ = TCD_INPUTMODE_EDGETRIGFREQ_gc, /* Stop output on edge, maintain frequency */ INPUTMODE_LVLTRIGFREQ = TCD_INPUTMODE_LVLTRIGFREQ_gc /* Stop output at level, maintain frequency */ } INPUTMODE; /* Delay trigger select */ typedef enum { DLYTRIG_CMPASET = TCD_DLYTRIG_CMPASET_gc, /* Compare A set */ DLYTRIG_CMPACLR = TCD_DLYTRIG_CMPACLR_gc, /* Compare A clear */ DLYTRIG_CMPBSET = TCD_DLYTRIG_CMPBSET_gc, /* Compare B set */ DLYTRIG_CMPBCLR = TCD_DLYTRIG_CMPBCLR_gc /* Compare B clear */ } DLYTRIG; /* Delay select */ typedef enum { DLYSEL_OFF = TCD_DLYSEL_OFF_gc, /* No delay */ DLYSEL_INBLANK = TCD_DLYSEL_INBLANK_gc, /* Input blanking enabled */ DLYSEL_EVENT = TCD_DLYSEL_EVENT_gc /* Event delay enabled */ } DLYSEL; /* TCD.INTCTRL bit masks and bit positions */ typedef enum { INTCTRL_OVF = TCD_OVF_bm, /* Overflow interrupt enable bit mask. */ INTCTRL_TRIGA = TCD_TRIGA_bm, /* Trigger A interrupt enable bit mask. */ INTCTRL_TRIGB = TCD_TRIGB_bm /* Trigger B interrupt enable bit mask. */ } INTCTRL; /* TCD.INTFLAGS bit masks and bit positions */ typedef enum { INTFLAGS_OVF = TCD_OVF_bm, /* Overflow interrupt enable bit mask. */ INTFLAGS_TRIGA = TCD_TRIGA_bm, /* Trigger A interrupt enable bit mask. */ INTFLAGS_TRIGB = TCD_TRIGB_bm /* Trigger B interrupt enable bit mask. */ } INTFLAGS; /* TCD.STATUS bit masks and bit positions */ typedef enum { STATUS_ENRDY = TCD_ENRDY_bm, /* Enable ready bit mask. */ STATUS_CMDRDY = TCD_CMDRDY_bm, /* Command ready bit mask. */ STATUS_PWMACTA = TCD_PWMACTA_bm, /* PWM activity on A bit mask. */ STATUS_PWMACTB = TCD_PWMACTB_bm /* PWM activity on B bit mask. */ } STATUS; /* TCD.FAULTCTRL bit masks and bit positions */ typedef enum { FAULTCTRL_CMPA = TCD_CMPA_bm, /* Compare A value bit mask. */ FAULTCTRL_CMPB = TCD_CMPB_bm, /* Compare B value bit mask. */ FAULTCTRL_CMPC = TCD_CMPC_bm, /* Compare C value bit mask. */ FAULTCTRL_CMPD = TCD_CMPD_bm, /* Compare D vaule bit mask. */ FAULTCTRL_CMPAEN = TCD_CMPAEN_bm, /* Compare A enable bit mask. */ FAULTCTRL_CMPBEN = TCD_CMPBEN_bm, /* Compare B enable bit mask. */ FAULTCTRL_CMPCEN = TCD_CMPCEN_bm, /* Compare C enable bit mask. */ FAULTCTRL_CMPDEN = TCD_CMPDEN_bm /* Compare D enable bit mask. */ } FAULTCTRL; /* Type of Callback Function */ typedef void (*callback_t)(INTFLAGS flags); Tcd(void) { } /* virtual */ ~Tcd(void) { } static void begin(WGMODE wgmode = WGMODE_ONERAMP, CLKSEL clksel = CLKSEL_OSCHF, SYNCPRES syncpres = SYNCPRES_DIV1, CNTPRES cntpres = CNTPRES_DIV1) { end(); TCD0.CTRLB = wgmode; TCD0.CTRLC = TCD_AUPDATE_bm; TCD0.CTRLD = 0; TCD0.CTRLE = 0; TCD0.EVCTRLA = 0; TCD0.EVCTRLB = 0; TCD0.INTCTRL = 0; TCD0.INTFLAGS = 0xFF; TCD0.STATUS = 0xFF; TCD0.INPUTCTRLA = 0; TCD0.INPUTCTRLB = 0; TCD0.FAULTCTRL = 0; TCD0.DLYCTRL = 0; TCD0.DLYVAL = 0; TCD0.DITCTRL = 0; TCD0.DITVAL = 0; TCD0.DBGCTRL = 0; TCD0.CMPASET = 0; TCD0.CMPBSET = 0; TCD0.CMPACLR = 0; TCD0.CMPBCLR = 0; TCD0.CTRLA = clksel | cntpres | syncpres; _frequency = 0; _callback = 0; } static void end(void) { wait(TCD_ENRDY_bm); TCD0.CTRLA = 0; } static void dbgctrl(bool dbgrun = true, bool faultdet = true) { /* Double-Buffered Registers */ TCD0.DBGCTRL = (TCD0.DBGCTRL & ~(TCD_FAULTDET_bm | TCD_DBGRUN_bm)) | (faultdet ? TCD_FAULTDET_bm : 0) | (dbgrun ? TCD_DBGRUN_bm : 0); synchronize(); } static void output(CMP cmp, bool fcmpval = false, bool enable = true) { /* Static Registers */ uint8_t cmpen = FAULTCTRL_CMPAEN << cmp; uint8_t cmpval = FAULTCTRL_CMPA << cmp; faultctrl(cmpen | cmpval, enable ? (fcmpval ? cmpen | cmpval : cmpen) : 0); } static void output(CMPCSEL cmpc = CMPCSEL_PWMA, CMPDSEL cmpd = CMPDSEL_PWMB) { /* Static Registers */ TCD0.CTRLC = (TCD0.CTRLC & ~(TCD_CMPDSEL_bm | TCD_CMPCSEL_bm)) | cmpd | cmpc; } static void cmpovr(bool enable = true, uint8_t cmpaval = 0b1010, uint8_t cmpbval = 0b1010) { /* Static Registers */ if ((TCD0.CTRLA & TCD_WGMODE_gm) == WGMODE_ONERAMP) { cmpaval = (cmpaval & 0b0001 ? 0b0010 : 0) | (cmpaval & 0b0010 ? 0b0001 : 0); cmpbval = (cmpbval & 0b0001 ? 0b1000 : 0) | (cmpbval & 0b0010 ? 0b0100 : 0); } TCD0.CTRLC = (TCD0.CTRLC & ~TCD_CMPOVR_bm) | (enable ? TCD_CMPOVR_bm : 0); TCD0.CTRLD = ((cmpbval << TCD_CMPBVAL_gp) & TCD_CMPBVAL_gm) | ((cmpaval << TCD_CMPAVAL_gp) & TCD_CMPAVAL_gm); } static void fifty(bool enable = true) { /* Static Registers */ TCD0.CTRLC = (TCD0.CTRLC & ~TCD_FIFTY_bm) | (enable ? TCD_FIFTY_bm : 0); } static void dither(DITHERSEL sel, uint8_t val, bool sync = true) { /* Double-Buffered Registers */ TCD0.DITCTRL = sel; TCD0.DITVAL = val > TCD_DITHER_gm ? TCD_DITHER_gm : val; if (sync) synchronize(); } static void compare(CMP cmp, uint16_t set, uint16_t clr) { /* Double-Buffered Registers */ switch (cmp) { case CMPA: TCD0.CMPASET = set; TCD0.CMPACLR = clr; break; case CMPB: TCD0.CMPBSET = set; TCD0.CMPBCLR = clr; break; /* Auto Update */ default: break; } } static uint16_t count(uint32_t freq, bool diten = false) { uint32_t cnt = frequency(); uint8_t dit; if (diten) { cnt = (cnt << 4) / freq; dit = (uint8_t)(cnt & 0x0F); cnt >>= 4; } else { cnt = cnt / freq; dit = 0; } dither(DITHERSEL_ONTIMEAB, dit, false); return cnt > MAX_COUNT ? MAX_COUNT : cnt - 1; } static void pwm(uint16_t count, uint16_t duty, uint8_t rise = 0, uint8_t fall = 0) { if (duty > MAX_COUNT) duty = MAX_COUNT; uint16_t set = count - rise - fall; set -= (uint32_t)set * duty / MAX_COUNT; compare(CMPA, set + rise, count - fall); compare(CMPB, set, count); } static void event(CMP cmp, bool enable = true, CFG cfg = CFG_NEITHER, EDGE edge = EDGE_FALL_LOW, ACTION action = ACTION_FAULT) { /* Static Registers */ switch (cmp) { case CMPA: TCD0.EVCTRLA = cfg | edge | action | (enable ? TCD_TRIGEI_bm : 0); break; case CMPB: TCD0.EVCTRLB = cfg | edge | action | (enable ? TCD_TRIGEI_bm : 0); break; default: break; } } static void input(CMP cmp, INPUTMODE mode) { /* Static Registers */ switch (cmp) { case CMPA: TCD0.INPUTCTRLA = mode; break; case CMPB: TCD0.INPUTCTRLB = mode; break; default: break; } } static void delay(DLYPRESC presc, DLYTRIG trig, DLYSEL sel, uint8_t val, bool sync = true) { /* Double-Buffered Registers */ TCD0.DLYCTRL = presc | trig | sel; TCD0.DLYVAL = val; if (sync) synchronize(); } static void swcapture(CMP cmp) { switch (cmp) { case CMPA: command(CMD_SCAPTUREA); break; case CMPB: command(CMD_SCAPTUREB); break; default: break; } } static uint16_t capture(CMP cmp) { switch (cmp) { case CMPA: return TCD0.CAPTUREA; case CMPB: return TCD0.CAPTUREB; default: break; } return 0; } static STATUS status(void) { return (STATUS)TCD0.STATUS; } static void run(void) { wait(TCD_ENRDY_bm); TCD0.CTRLA |= TCD_ENABLE_bm; } static void stop(void) { command(CMD_DISEOC); } static void restart(void) { command(CMD_RESTART); } static void callback(callback_t func) { _callback = func; } static void interrupt(INTCTRL ctrl, bool enable = true) { if (enable) { TCD0.INTFLAGS = ctrl; #if CONFIG_TCD_ISR TCD0.INTCTRL |= ctrl; #endif } else { #if CONFIG_TCD_ISR TCD0.INTCTRL &= ~ctrl; #endif TCD0.INTFLAGS = ctrl; } } static void poll(void) { #if !CONFIG_TCD_ISR isr(); #endif } private: /* TCD.CTRLE bit masks and bit positions */ typedef enum { CMD_SYNCEOC = TCD_SYNCEOC_bm, /* Synchronize end of cycle strobe bit mask. */ CMD_SYNC = TCD_SYNC_bm, /* synchronize strobe bit mask. */ CMD_RESTART = TCD_RESTART_bm, /* Restart strobe bit mask. */ CMD_SCAPTUREA = TCD_SCAPTUREA_bm, /* Software Capture A Strobe bit mask. */ CMD_SCAPTUREB = TCD_SCAPTUREB_bm, /* Software Capture B Strobe bit mask. */ CMD_DISEOC = TCD_DISEOC_bm, /* Disable at end of cycle bit mask. */ } CMD; static uint32_t _frequency; static callback_t _callback; #if CONFIG_TCD_ISR friend void tcd_isr(void); #endif static inline void isr(void) { uint8_t flags = TCD0.INTFLAGS = TCD0.INTFLAGS; if (flags && _callback) _callback((INTFLAGS)flags); } static void faultctrl(/* FAULTCTRL */ uint8_t mask, /* FAULTCTRL */ uint8_t flag) { /* Static Registers */ _PROTECTED_WRITE(TCD0.FAULTCTRL, (TCD0.FAULTCTRL & ~mask) | flag); } static void synchronize(bool eoc = true) { command(eoc ? CMD_SYNCEOC : CMD_SYNC); } static void command(CMD cmd) { wait(TCD_CMDRDY_bm); TCD0.CTRLE = cmd; } static void wait(uint8_t status) { while ((TCD0.STATUS & status) == 0) yield(); } static uint32_t frequency(void) { if (_frequency == 0) { uint32_t clk = 0; switch (TCD0.CTRLA & TCD_CLKSEL_gm) { case CLKSEL_OSCHF : clk = Fuse::OSCCFG::frequency(); break; #if !defined(__AVR_1__) case CLKSEL_PLL : clk = Clock::pllfreq(); break; #endif case CLKSEL_EXTCLK: clk = CONFIG_EXTCLK; break; case CLKSEL_CLKPER: clk = Clock::frequency(); break; } switch (TCD0.CTRLA & TCD_CNTPRES_gm) { default: break; case TCD_CNTPRES_DIV4_gc : clk >>= 2; break; case TCD_CNTPRES_DIV32_gc: clk >>= 5; break; } _frequency = clk; } return _frequency; } }; #endif |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
/* avr8_tcd.h - TCD Driver for Microchip AVR8 Series Copyright (c) 2026 Sasapea's Lab. All right reserved. This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with this program. If not, see <https://www.gnu.org/licenses/>. */ #include "avr8_tcd.h" #if defined(TCD0) const uint16_t Tcd::MAX_COUNT = 0x0FFF; uint32_t Tcd::_frequency; Tcd::callback_t Tcd::_callback; #if CONFIG_TCD_ISR inline void tcd_isr(void) { Tcd::isr(); } ISR(TCD0_OVF_vect) { tcd_isr(); } ISR(TCD0_TRIG_vect) { tcd_isr(); } #endif #endif |
【関連投稿】
Microchip AVR8 用のライブラリを自作する。(GPIO)
Microchip AVR8 用のライブラリを自作する。(FUSE)
Microchip AVR8 用のライブラリを自作する。(CLOCK)
Microchip AVR8 用のライブラリを自作する。(RESET)
Microchip AVR8 用のライブラリを自作する。(PORTMUX)
Microchip AVR8 用のライブラリを自作する。(USART)
Microchip AVR8 用のライブラリを自作する。(RTC)
Microchip AVR8 用のライブラリを自作する。(TCA)
Microchip AVR8 用のライブラリを自作する。(TCB)
Microchip AVR8 用のライブラリを自作する。(VREF)
Microchip AVR8 用のライブラリを自作する。(DAC)
Microchip AVR8 用のライブラリを自作する。(AC)
Microchip AVR8 用のライブラリを自作する。(ADC)
Microchip AVR8 用のライブラリを自作する。(ZCD)
Microchip AVR8 用のライブラリを自作する。(SPI)
Microchip AVR8 用のライブラリを自作する。(TWI)
Microchip AVR8 用のライブラリを自作する。(MAIN)
Microchip AVR8 用のライブラリを自作する。(CONFIG)
Microchip AVR8 用のライブラリを自作する。(ALARM)
Microchip AVR8 用のライブラリを自作する。(TASK)
Microchip AVR8 用のライブラリを自作する。(CCL)
Microchip AVR8 用のライブラリを自作する。(TCD)
Microchip AVR8 用のライブラリを自作する。(DOWNLOAD)
